Answers to Study Questions

1. What is the definition of the vorticity?
   ans:    The curl of the velocity, Ñ×[u\vec]
    
2. What is the physical meaning of the vorticity?
   ans:    Rate of rotation of a fluid element about its center of mass.
    
3. What does it mean for a fluid to be irrotational?
   ans:    Vorticity is zero.
    
4. According to Crocco's relation, under what conditions will an inviscid fluid be irrotational?
   ans:    Steady, adiabatic, no curved shocks or shock intersections.
    
5. List two flow features on a supersonic airfoil that will invalidate the irrotational assumption.
   ans:    Bow shock if present, flow within the boundary layers.
    
6. Why are irrotational flows easier to analyze than general rotational flows?
   ans:    The momentum equation can be replaced with the condition [(w)\vec] = 0
    
7. What is the definition of the velocity potential?
   ans:    [u\vec] = Ñf
    
8. Does a velocity potential exist for every possible flow? Explain your answer.
   ans:    No. The potential will exist only if the flow is irrotational.
    
9. The velocity potential guarantees what property of the velocity field?
   ans:    Irrotational.
    
10. What significant complication is present in the compressible potential equation that is absent in the incompressible analog?
    ans:    Non-linearity.
     
11. What is the motivation behind the small perturbation assumption?
    ans:    Remove the non-linearity from the potential equation.
     
12. What is the perturbation velocity potential? How is it related to the full velocity potential?
    ans The potential that gives rise to the perturbation velocities. F = U_¥ x + f.
     
13. What major simplification is made in going from the full velocity potential to the perturbation potential equation?
    ans:    The perturbation potential equation is linear.
     
14. For what Mach number ranges is the perturbation potential equation valid?
    ans:    M_¥ £ 0.8, 1.2 £ M_¥ £ 5.
     
15. What geometrical constraints are imposed on an airfoil shape if it is to be analyzed with linear (small perturbation) theory?
    ans:    It must be thin and flying at low angle of attack.
     
16. State the formula for the linearized pressure coefficient.
    ans:    C_p = -2u/U_¥
     
17. How can a compressible subsonic flow be related to an incompressible flow?
    ans:    Through the Prandtl-Glauert similarity rule, i.e. f = [`(f)]/Ö{1-M<sub>¥</sub><sup>2</sup>}, where f is the disturbance potential at M<sub>¥</sub> and [`(f)] is the disturbance potential at M = 0.
     
18. What is the utility of the Prandtl-Glauert similarity rule?
    ans:    It relates the flow at M_¥ £ 0.8 to the incompressible flow around the same body.
     
19. What is the Prandtl-Glauert compressibility correction?
    ans:    C_p = C_P0/Ö{1-M_¥²}, where C_p is the pressure coefficient at M_¥ and C_p is the pressure coefficient at M_¥ = 0.
     
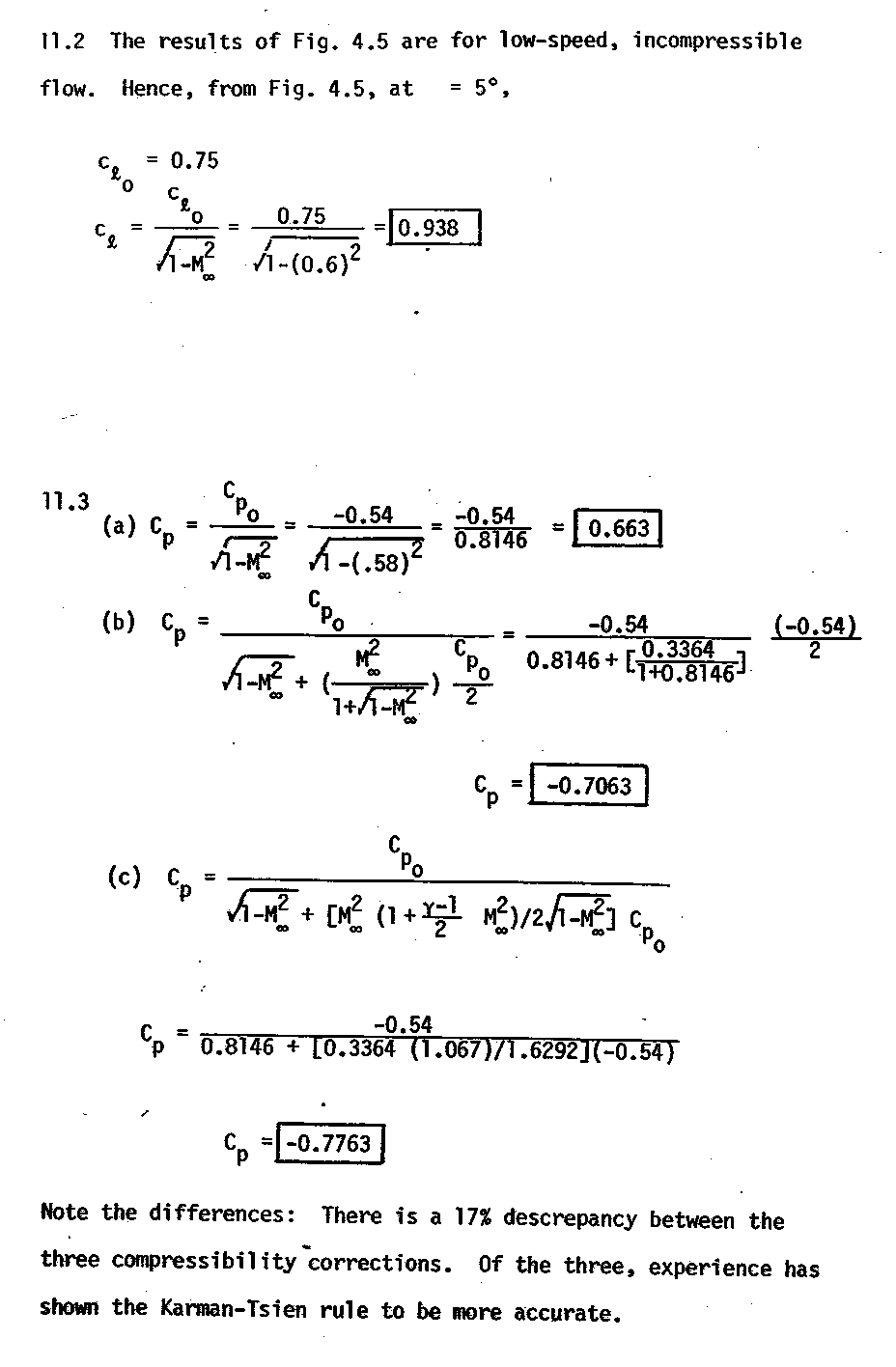
20. Why are the improved compressibility corrections (i,e, Karman-Tsien) more accurate?
    ans:    since they account for the local variations in Mach number (higher order corrections).